Medición de distancia entre dos observaciones
Capítulo 15 del libro Data Minig for Business Analytics: Concepts, Techniques, and Applications with XlMiner, Third Edition, Galit Shmuleli, Peter C. Bruce, and Nitin R. Patel.
15.2
Medición de distancia entre dos observaciones
Denotamos
a dij como una métrica de distancia, o medida de disimilitud, entre las
observaciones i y j. Para la observación i tenemos el vector de mediciones (xi1,
xi2, xi3,…,xip), mientras que para la
observación j tenemos el vector de mediciones (xj1, xj2,
xj3,…,xjp). Por ejemplo, podemos escribir el vector de
medición para el Servicio Público de Arizona como [1.06, 9.2, 151, 54.4, 1.6,
9007, 0,0.628].
Las
distancias pueden ser definidas en múltiples formas, pero en general, se requieren las
siguientes propiedades:
- No
Negativa: dij > 0
- Proximidad
misma: dij = 0
- Simetría:
dij = dji
- Desigualdad
triangular: dij< = dik + dkj (la distancia
entre cualquier par no excede la suma de distancias entre los otros dos pares).
Distancia
Euclidiana
La
más popular medida de distancia es la Distancia Euclidiana, dij, la
cual, entre dos observaciones, i y j, es definida así:
dij = √(xi1
- xj1)2 + (xi2 - xj2)2+…+(xip – xjp)2
Por
ejemplo, la distancia Euclidiana entre Servicio Público Arizona y Boston Edison
Co. puede ser calculada a partir de la data bruta así:
dij
= √(1.06-0-89)2 + (9.2-10.3)2+(151-202)2+…+(0.628-1.555)2
=
3989.408
.
Normalizando
la medición numérica
La medida calculada anteriormente es altamente influencia por la escala de cada variable, tal que las variables con escalas grandes (por ejemplo: Ventas) tiene mucha mayor influencia sobre la distancia total. Por lo tanto, es usual normalizar las mediciones continuas antes de calcular la distancia Euclidiana. Esto convierte todas las mediciones a la misma escala. Normalizar una medición significa sustraer el promedio y dividir sobre la desviación estándar (los valores normalizados son también llamadas z-scores). Por ejemplo, el promedio de las ventas de las 22 entidades públicas es 8914.045 y la desviación estándar es 3549.984. Las ventas normalizadas para Servicio Público de Arizona, es entonces (ver tabla 15.1): (9077-8914.045)/3549.984 = 0.046
Regresando a las data simplificada de las entidades con sólo dos mediciones (Ventas y Costo de combustible), primero normalizamos las mediciones (ver tabla 15.2), y luego calculamos la distancia Euclideana entre cada par. La tabla 15.3 nos muestra las distancias por pares de las primeras cinco entidades. Una tabla similar debe ser construida para las 22 entidades.
Otras medidas de distancia para la Data Numérica
Es importante advertir que la elección de la medida de distancia juega un rol importante en el análisis de cluster. La directriz principal es dependiente del dominio: ¿Que está siendo medido exactamente? ¿Cómo son relacionadas las distintas mediciones? ¿A qué escala debería ser tratada cada medición (numérica, ordinal o nominal)? ¿Hay outliers? Finalmente, dependiendo de los objetivos del análisis, ¿deberían los clusters ser distinguidos principalmente por un pequeño conjunto de mediciones, o deberían ellos ser separados por múltiples mediciones que pesan moderadamente?
A pesar de que la distancia Euclidiana es la más usada, ésta tiene tres principales características que necesitan tenerse en cuenta. Primero, como se mencionó anteriormente, es altamente dependiente de la escala. Cambiar la unidad de una variable (por ejemplo: de centavos a dólares) puede tener una gran influencia en los resultados. La normalización es, por lo tanto, una solución común. Pero la ponderación desigual debería ser considerada si queremos que los clusters dependan más de ciertas mediciones y menos de otras. La segunda característica de la distancia Euclidiana es que ésta ignora completamente la relación entre las mediciones. Así, si las mediciones son de hecho fuertemente corelacionadas, una distancia diferente (por ejemplo: la distancia estadística, descrita a continuación) es probable que sea una mejor opción. Tercero, la distancia Euclidiana es sensitiva a los outliers. Si se cree que la data contiene outliers y la eliminación cuidadosa de estos no es una opción, el uso de una distancia más fuerte (por ejemplo: la distancia Manhattan descrita a continuación) es preferible.
Adicionales métricas de distancia populares son usadas a menudo (por razones como las describimos anteriormente):
Similitud basada en la corelación
Algunas veces es más natural o conveniente trabajar con una medida de similitud entre las observaciones que con la distancia, que mide la disimilitud. Una medida de similitud popular es el cuadrado del coeficiente corelacionado de Pearson, r2ij, donde el coeficiente de corelación es definido por:
Tales medidas pueden siempre ser convertidas a medidas de distancia. En el ejemplo anterior podríamos definir una medida de distancia dij = 1- r2ij
Distancia estadística (también llamada distancia Mahalanobis)
Esta métrica tiene una ventaja sobre las otras métricas mencionadas en que ésta toma en cuenta la correlación entre las mediciones. Con esta métrica, las mediciones que son altamente corelacionadas con otras mediciones no contribuyen tanto como aquellas que no son corelacionadas o son medianamente corelacionadas. La distancia estadística entre las observaciones i y j es definida como:
dij = √(xi - xj)' S-1
(xi - xj),
donde xi y xj son vectores p-dimensionales de los valores de las mediciones para las observaciones i y j, respectivamente, y S es la matriz de co-varianza para esos vectores. (', una operación de transponer, simplemente convierte un vector de columna en un vector de fila). S-1 es la matriz inversa de S, que es la extensión de la dimensión p a la división.Distancia Manhattan (city block)
Esta distancia mira las diferencias absolutas en vez de las diferencias cuadradas, y es definida por:
Distancia máxima de coordenadas
Esta distancia mira sólo las mediciones en las cuales las observaciones i y j se desviaron más. Es definida mediante:
Medidas de distancia para la data categórica
En el caso de mediciones con valores binarios, es más intuitivamente atractivo usar medidas de similitud que de distancia. Supongamos que tenemos valores binarios para todas las xij's, y para las observaciones i y j tenemos las siguiente tabla 2 x 2:
donde a denota el número de variables para el cual las observaciones i y j no tienen ese atributo (cada uno de ellos tiene valor 0 en ese atributo), d es el número de variables para el cual las dos observaciones tienen el atributo presente, y así. Las medidas de similitud más usadas en esta situación son:
Coeficiente de pares (a + d) / n
Coeficiente Jaccard's d / (b + c + d)
Este coeficiente ignora los ceros pares. Es deseable cuando no queremos considerar que dos personas sean similares simplemente porque un gran número de características están ausentes en ambas. Por ejemplo, si 'posee una corbata' es una de las variables, un par de 'sí' podría ser una evidencia de similitud, pero un par de 'no' nos dice poco sobre si las dos personas son similares.
Medidas de distancia para Data Mixta
Cuando las mediciones son mixtas (algunas continuas y otras binarias), un coeficiente similar sugerida por Gower es muy útil. La medida similar de Gower es un promedio ponderado de las distancias calculadas para cada variable, después de escalar cada variable a una escala de [0,1]. Es definida como:
donde sijm es la similitud entre las observaciones i y j sobre las mediciones m, y wijm es un peso binario dado a las distancias correspondientes.
Las medidas de similitud sijm y peso wijm son calculadas de la siguiente manera:
1. Para mediciones continuas, sijm = 1 - |xim- xjm| / [max (xm) - min (xm)] y wijm = 1 a menos que el valor para la medición m sea desconocido en una o ambas observaciones, en cuyo caso wijm = 0.
2. Para mediciones binarias, sijm = 1 si xim = xjm = 1 y 0 de otra manera. wijm = 1 a menos que xim = xjm = 0
3. Para mediciones categóricas no binarias, sijm = 1 si ambas observaciones están en la misma categoría, y de otra manera, sijm = 0. Como en las mediciones continuas, wijm = 1 a menos que la categoría para la medición m sea desconocido en una o ambas observaciones, en cuyo caso wijm = 0
Siguiente contenido>> 15.3 Medición de distancia entre dos clusters


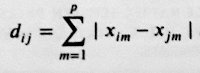





Comentarios
Publicar un comentario